Plate and Shell Optimization using Multi-Patch IGA
1. Topology Optimization of plates and shells
While Topology Optimization (TO) has seen immense growth over the last three decades, the vast majority of research has focused on 2D and 3D continuum solids. These problems are governed by second-order Partial Differential Equations (PDEs), which only require $C^0$ continuity (simple displacement connectivity).
However, high-performance thin structures like plates and shells (based on Kirchhoff-Love theory) are governed by fourth-order PDEs. These require $C^1$ continuity—meaning not only must the displacements match at the boundaries, but the slopes (derivatives) must be continuous as well.
In traditional Finite Element Analysis (FEA), elements are inherently $C^0$ at their edges. Achieving $C^1$ continuity in FEM requires complex “Hermite” elements or additional rotational degrees of freedom (DOFs), which often lead to shear locking or high computational overhead. Consequently, TO for 4th-order structures remained a niche and difficult field.
2. IGA-based spline basis functions
Isogeometric Analysis changes this landscape fundamentally. Because IGA uses splines (NURBS), it provides natural higher-order continuity (#) within a single patch. This allows for “rotation-free” plate and shell formulations, significantly simplifying the analysis of 4th-order structures.
Despite this advantage, IGA-based topology optimization for plates and shells is still relatively rare in the literature. Our work fills this critical gap.
3. Multi-Patch IGA and Strong Coupling
Real-world engineering structures are rarely composed of a single rectangular NURBS patch; they are multi-patch assemblies (e.g., an aircraft fuselage or a car body). By default, when two NURBS patches meet, they only share $C^0$ continuity. For 4th-order plate and shell problems, this $C^0$ connection is insufficient, as it creates “kinks” in the slope that invalidate the Kirchhoff-Love assumptions.
Our Solution: Strong C^1 Coupling
To solve this, we implemented a strong coupling framework 1. Instead of using penalty methods or Lagrange multipliers (which can be unstable), we modify the basis functions at the interface. The basis functions at the patch boundaries are reconstructed as a linear function of the existing basis functions. This mathematically “glues” the patches together such that C^1 continuity is strictly enforced across the entire interface, allowing the 4th-order physics to flow seamlessly from one patch to the next.
4. Multi-Patch Shell TO
This work represents a milestone in computational mechanics: the first implementation of multi-patch shell and plate topology optimization for 4th-order structures. By combining the strong coupling of patches with a density-based topology optimization framework, we can evolve optimal material layouts for complex, curved geometries that were previously impossible to optimize using standard IGA or FEM tools.
Integration with AMR
To further push the boundaries of efficiency, we integrated Adaptive Mesh Refinement (AMR).
- The system identifies high-gradient regions at the material interfaces.
- It dynamically refines the spline space only where the “material evolution” is happening.
- This ensures that the optimized boundaries of the plate or shell are smooth and precise, while keeping the total number of degrees of freedom to a minimum.
5. Methodology
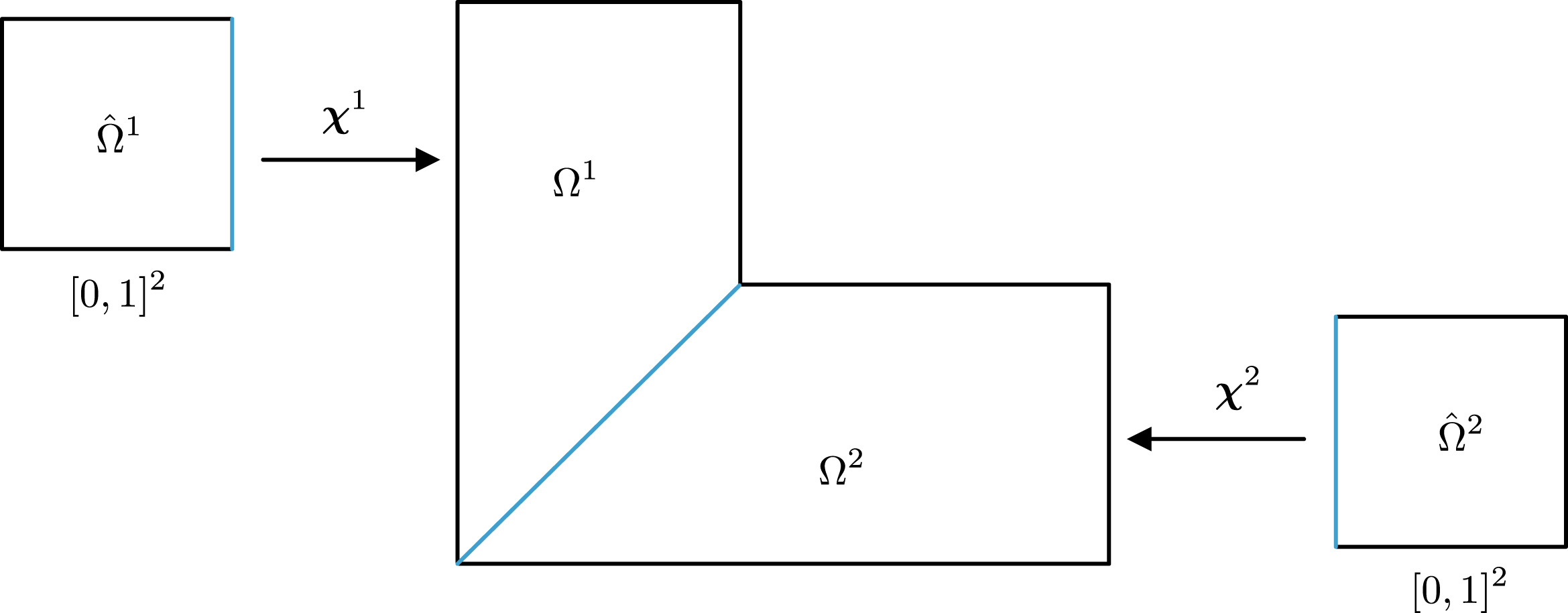
- Identification of basis functions near patch boundary responsible for $C^0$ continuity and marking their respective location.
- Generation of new $C^0$ basis functions from pre-existing $C^0$ bases following a linear combination approach.
- Removing the $C^0$ bases and inserting new polynomial functions that essentially satisfy $C^0$ continuity across the multi-patch domain.

Algorithm for the $ \ C^1$ continuous multi-patch coupling method
6. Representative results
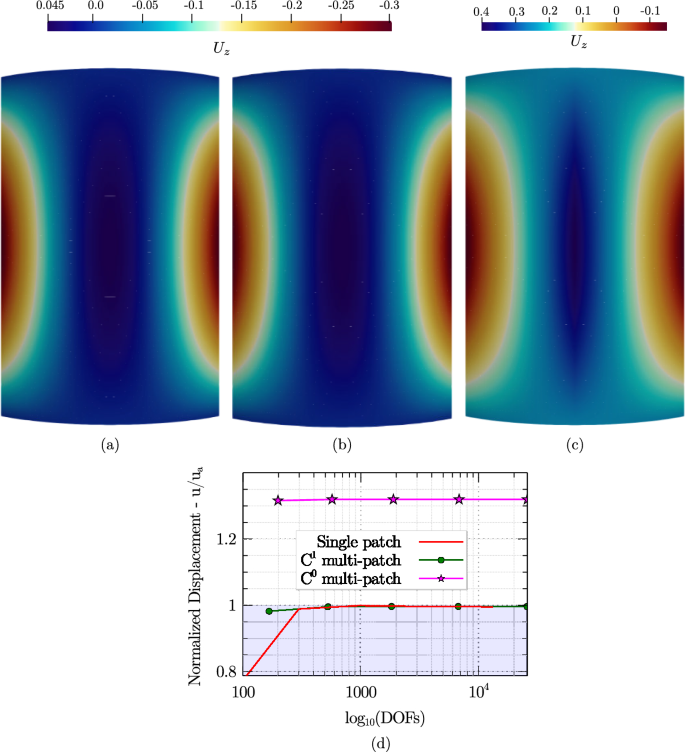
Verification of the multi-patch methodology on a Scordelis-Lo shell roof
Topology optimization of plate structures

Adaptively refining mesh in cantilever plate
Topology optimization of shell structures
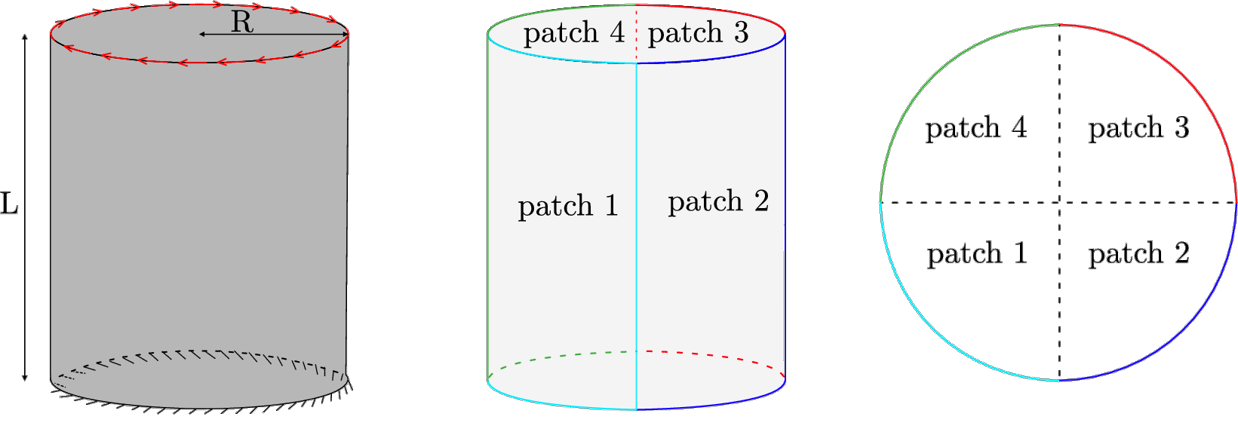

Topology optimization of multi-patch cylindrical shell
6. Key Contributions
- Multi-patch IGA framework for shell optimization
- Continuity-aware treatment of patch interfaces
- Application to curved shell and plate benchmark problems
- Combined the precision of IGA with the speed of AMR for complex shell problems.