Isogeometric Topology Optimization
A continuity-preserving framework for topology optimization using spline-based analysis
1. What is Structural Optimization?
Structural optimization is a mathematical approach used to find the best distribution of material within a defined space to sustain loads efficiently. It is generally categorized into three distinct levels of complexity:
| Type | What is Optimized? | Flexibility |
|---|---|---|
| Sizing Optimization | Dimensions of existing components (e.g., thickness of a beam, diameter of a bolt). | Low |
| Shape Optimization | The external contours or boundaries of a predefined geometry. | Medium |
| Topology Optimization | The layout, connectivity, and number of holes within the design space. | High |
2. Topology Optimization & SIMP
Topology Optimization (TO) is the most powerful of the three. It starts with a solid block of “virtual material” and mathematically “chisels” away the unnecessary parts.
The most common approach is the SIMP (Solid Isotropic Material with Penalization) method. In SIMP, we assign a density variable $\rho$ to every point in the domain:
- $\rho = 1$: Solid material.
- $\rho = 0$: Void (empty space).
- $0 < \rho < 1$: Intermediate “gray” material (penalized to drive it toward 0 or 1).
3. The Traditional Approach: FEM-Based TO
In traditional frameworks, the design domain is discretized using a Finite Element Method (FEM) mesh. The densities are typically defined element-wise, meaning each square or cube in the mesh has one single density value.
Issues with FEM-Based Optimization:
- Checkerboarding: Solutions often result in alternating solid/void cells that are physically impossible to manufacture.
- Mesh Dependency: Refining the mesh changes the final shape, meaning the solution isn’t objective.
- Jagged Boundaries: The final design has “pixelated” edges, requiring very fine meshes and manual cleanup in CAD software before manufacturing.
4. Isogeometric topology optimization (ITO)
Isogeometric Analysis (IGA) replaces the jagged elements of FEM with the smooth, high-order curves used in CAD: NURBS (Non-Uniform Rational B-Splines). Instead of assigning densities to elements, ITO formulates the framework directly on spline-based discretizations.
- Spline Representation: The optimized geometry is defined by control points. The density is no longer a “staircase” of blocks but a Continuous Density Function (CDF).
- Continuous Density: Because NURBS basis functions are C^k continuous (smoothly changing), the material density varies smoothly across the design domain. This naturally eliminates checkerboarding without needing complex artificial filters.
- Geometric Exactness: The boundaries are represented by smooth splines from the start. What you see in the optimization result is exactly what you can send to a CNC machine or 3D printer with minimal post-processing.
5. Methodology
In ITO, the material density field $\rho(\xi, \eta)$ is approximated using the same basis functions used for the structural analysis. This ensures a “continuous” transition of material:
\[\mathbb{X}(\xi, \eta) = \sum_{i=1}^{n} \sum_{j=1}^{m} R_{i,j}(\xi, \eta) \cdot \rho_{i,j}\]Where:
- $\mathbb{X}(\xi, \eta)$: The continuous density at any point in the parametric space.
- $R_{i,j}(\xi, \eta)$: The NURBS basis functions (ensuring $C^k$ continuity).
- $\rho_{i,j}$: The design variables (densities assigned to each control point), bounded such that $0 \le d_{i,j} \le 1$.
6. Representative results
Continuous topology optimization using IGA

In comparison with disrete-density FEM, continuous density function with IGA provides a smooth, manufacturable design for the same mesh.
Topology optimization of complex multi-patch structures with non-design domains
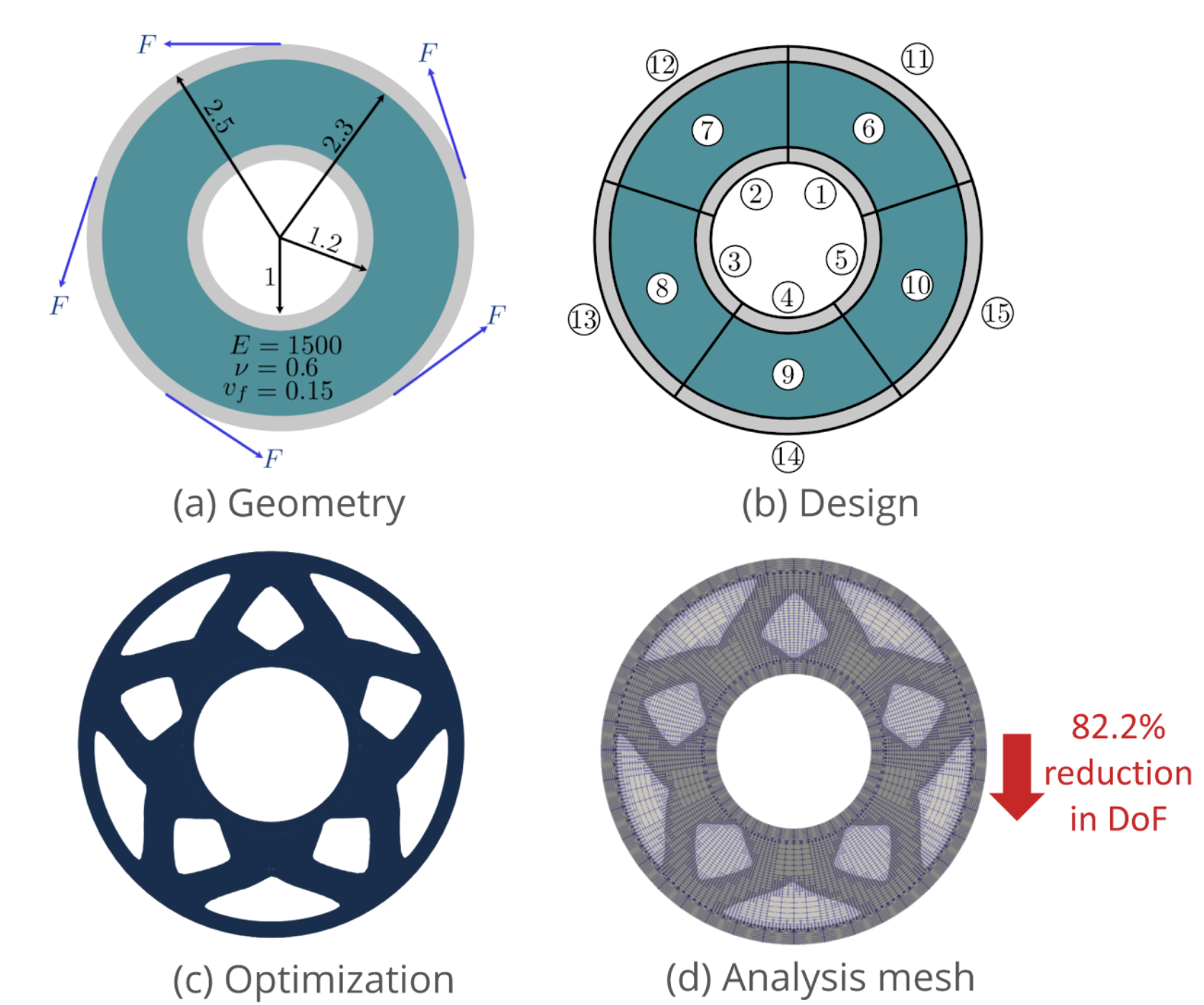
Optimization of complex 3D domains

Technical contributions
The key contributions of this project include:
- Development of a spline-based topology optimization framework using NURBS and multi-patch geometries
- Continuity-preserving sensitivity analysis within an isogeometric setting
- Efficient treatment of design variables defined directly on control points
- Demonstration of improved convergence behavior compared to classical finite element approaches