Adaptive Mesh Refinement
1. The Need for Adaptivity
Isogeometric Analysis (IGA) aims to unify Computer-Aided Design (CAD) and Finite Element Analysis (FEA) by using the same spline-based basis functions (like NURBS) for both geometry and simulation. In any mesh-based method such as FEA/IGA, accuracy is directly linked to the density of the mesh. High-stress areas, material interfaces, or complex topological boundaries require a very fine mesh. However, applying a fine mesh globally across the entire design domain leads to:
- Prohibitive Computational Costs: Massive increase in memory and CPU time.
- Redundancy: Wasting resources on regions with low gradients or simple physics.
Adaptive Mesh Refinement (AMR) solves this by dynamically identifying regions that require higher resolution and refining the mesh only in those specific areas.
2. The NURBS Bottleneck: Adaptivity in IGA
Standard IGA relies on NURBS (Non-Uniform Rational B-Splines). While NURBS are the industry standard for CAD, they possess a major flaw for simulation: Tensor Product Structure.
In a tensor product mesh, if you want to add a single knot (refinement) to increase detail in one corner, that knot must propagate across the entire row or column of the domain. This results in “global” refinement when only “local” refinement was intended.
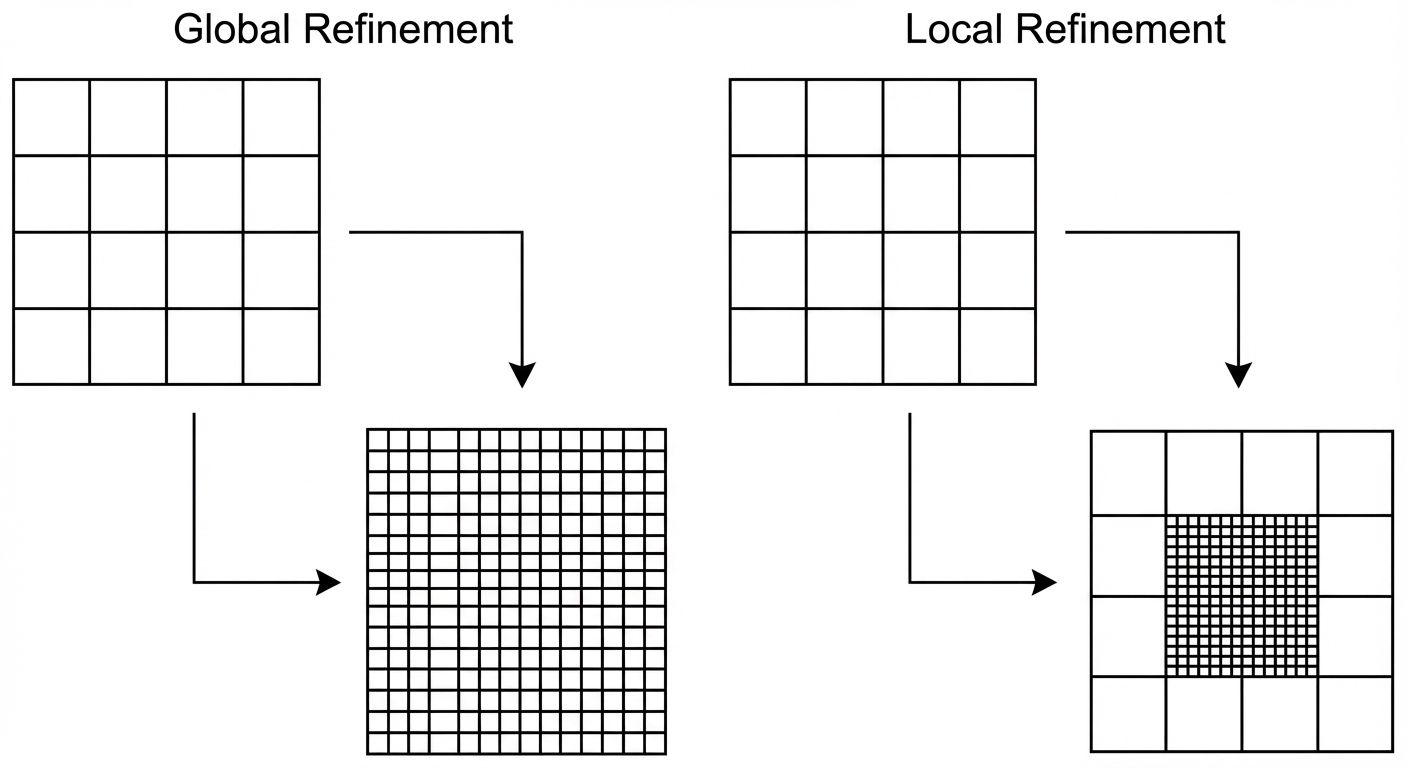
3. PHT-Splines: The Local Refinement Solution
To enable true AMR, we must move toward a different class of splines. PHT-Splines (Polynomial Splines over Hierarchical T-meshes) are specifically designed for this purpose.
Key Features of PHT-Splines:
- Hierarchical Structure: They utilize a “tree-based” data structure (similar to Quadtrees in 2D or Octrees in 3D).
- Local Refinement: You can refine a single element without affecting the rest of the mesh.
- Nested Spaces: Each level of refinement is mathematically nested within the previous one, ensuring stable convergence.
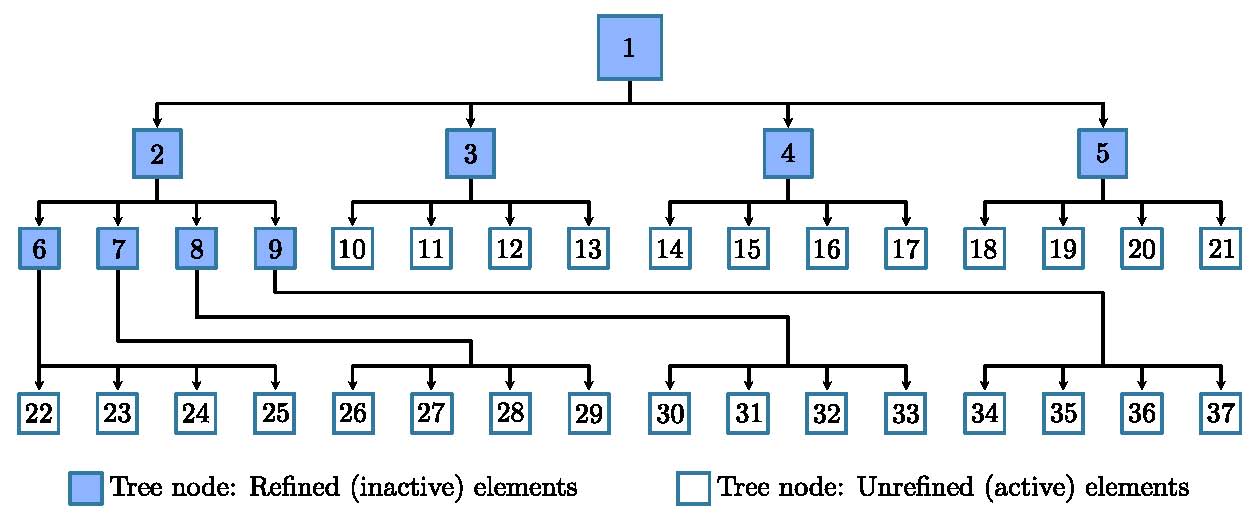
Tree structure of PHT-Splines
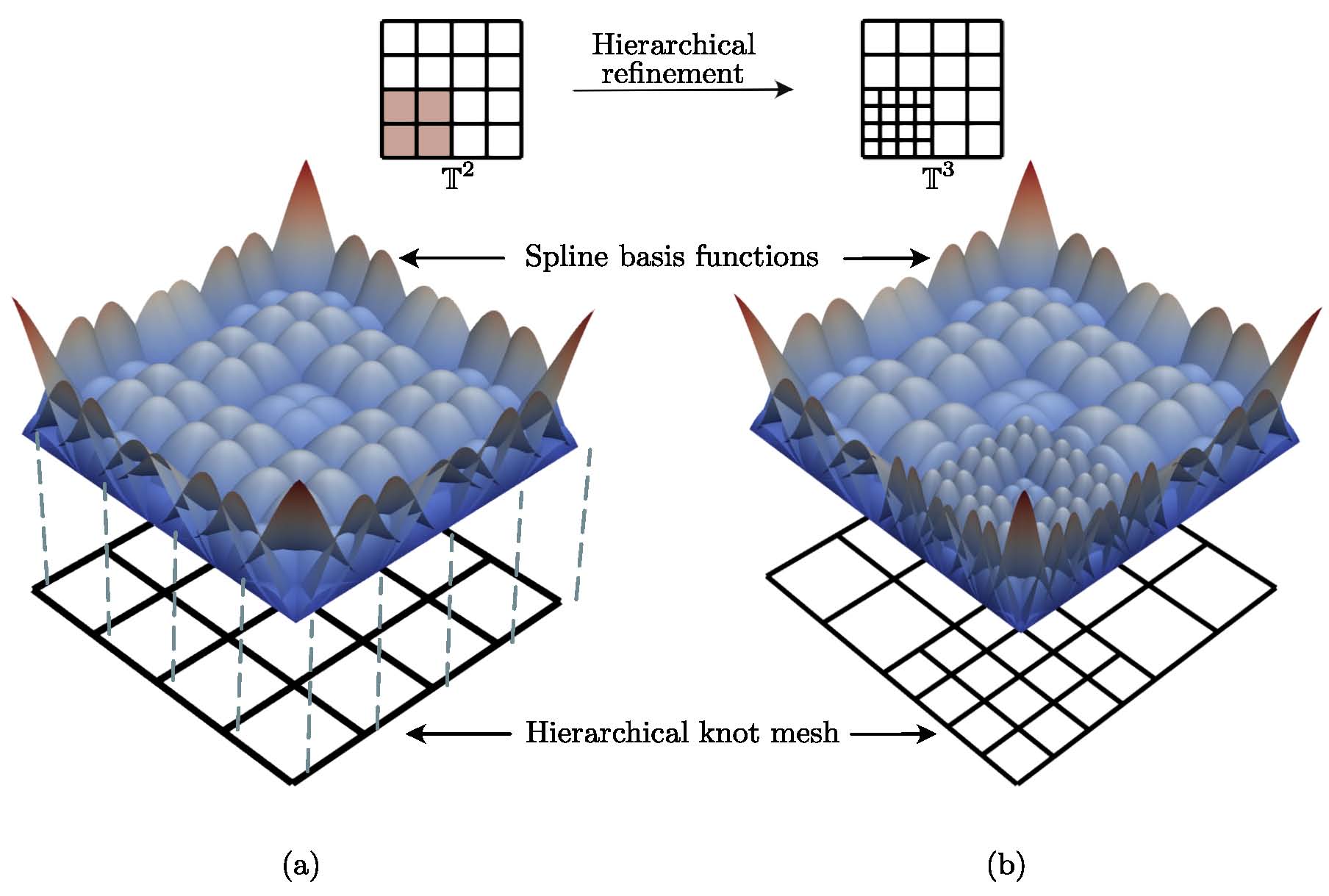
Local refinement in PHT-Splines
4. The GIFT Framework: Bridging CAD and PHT
A major conflict arises here: NURBS are essential for maintaining CAD consistency, but PHT-splines are necessary for efficient refinement. Simply switching to PHT-splines ruins the “Isogeometric” promise of using the original CAD geometry.
This is solved by the GIFT Framework (Geometry-Independent Field approximaTion).
How GIFT Works:
- Geometry Representation: The CAD geometry remains defined by its original NURBS description (ensuring perfect geometric accuracy).
- Field Approximation: The solution field (displacements, densities, etc.) is approximated using PHT-splines.
- Independence: Because the analysis field is mathematically independent of the geometric description, we can refine the PHT-mesh adaptively while the underlying CAD shape remains unchanged.
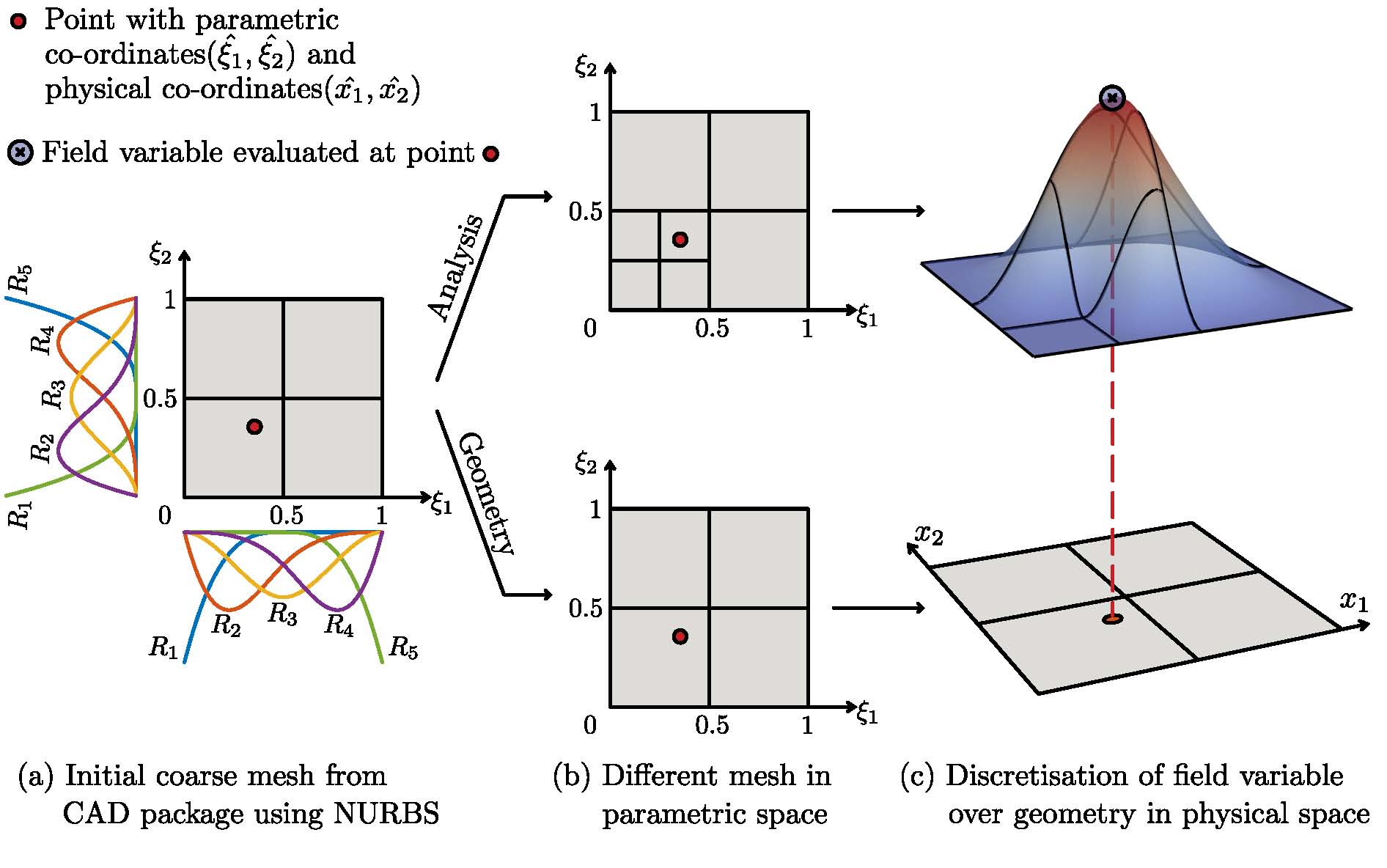
Idea of the GIFT framework
5. Performance in Topology Optimization
The application of Adaptive IGA using PHT-splines and the GIFT framework has shown transformative results in Topology Optimization problems.During the optimization process, the material boundaries shift. AMR allows the mesh to “follow” the evolving shape, refining only at the material interfaces where the densities are intermediate or the gradient is highest.
Proven Benefits:
- Significant Reduction in Degrees of Freedom (DOF): Achieve the same accuracy as a fine global mesh with up to 80–90% fewer equations.
- Reduced CPU Time: Faster solver iterations due to smaller system matrices.
- Memory Efficiency: Drastically lower memory footprint, allowing for higher-resolution designs on standard hardware.
- Optimized Element Count: Only placing elements where they contribute to the structural integrity of the design.
6. Representative results
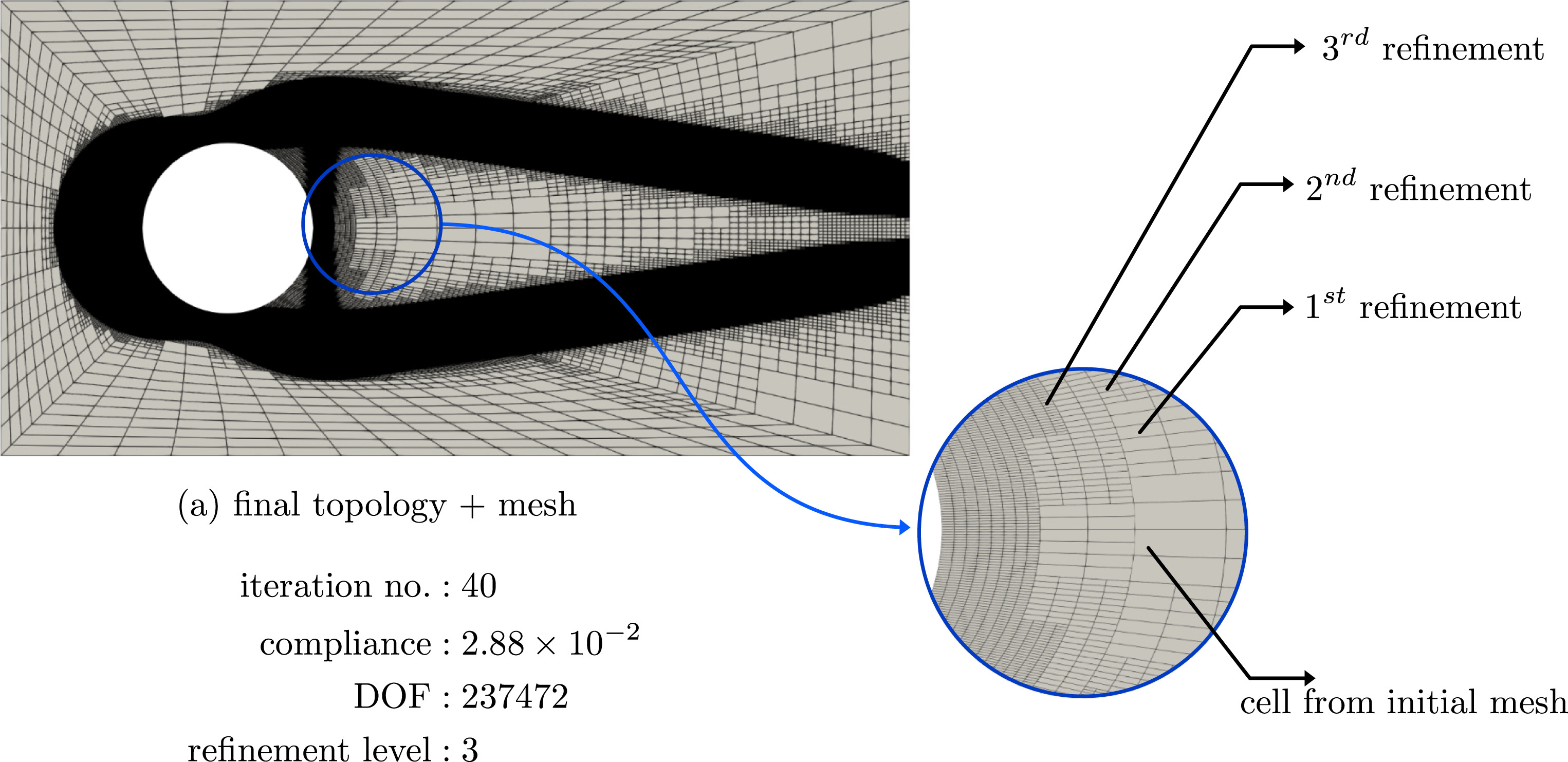
Adaptively refined mesh in a 2D plane stress problem
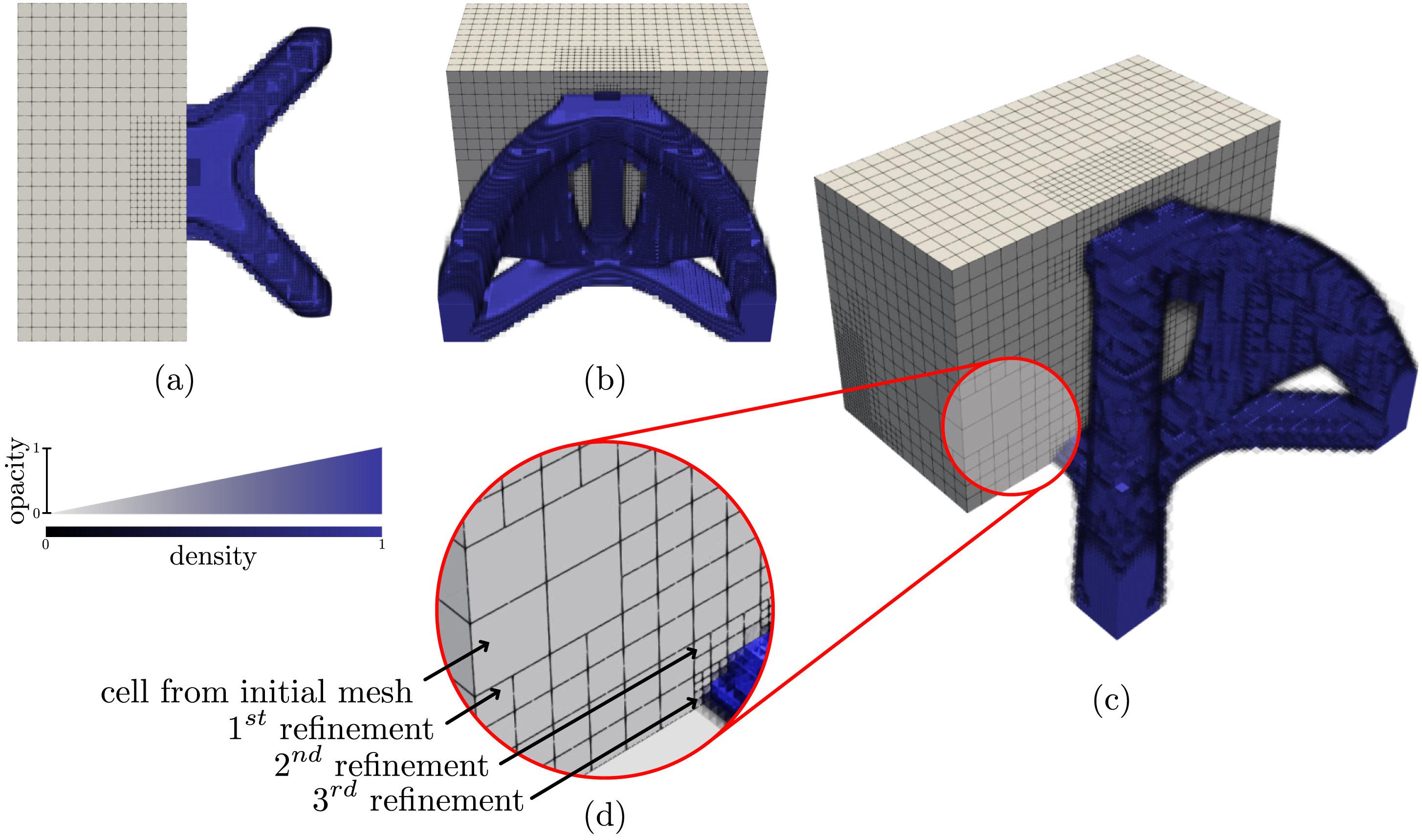
Adaptively refined mesh in a 3D domain
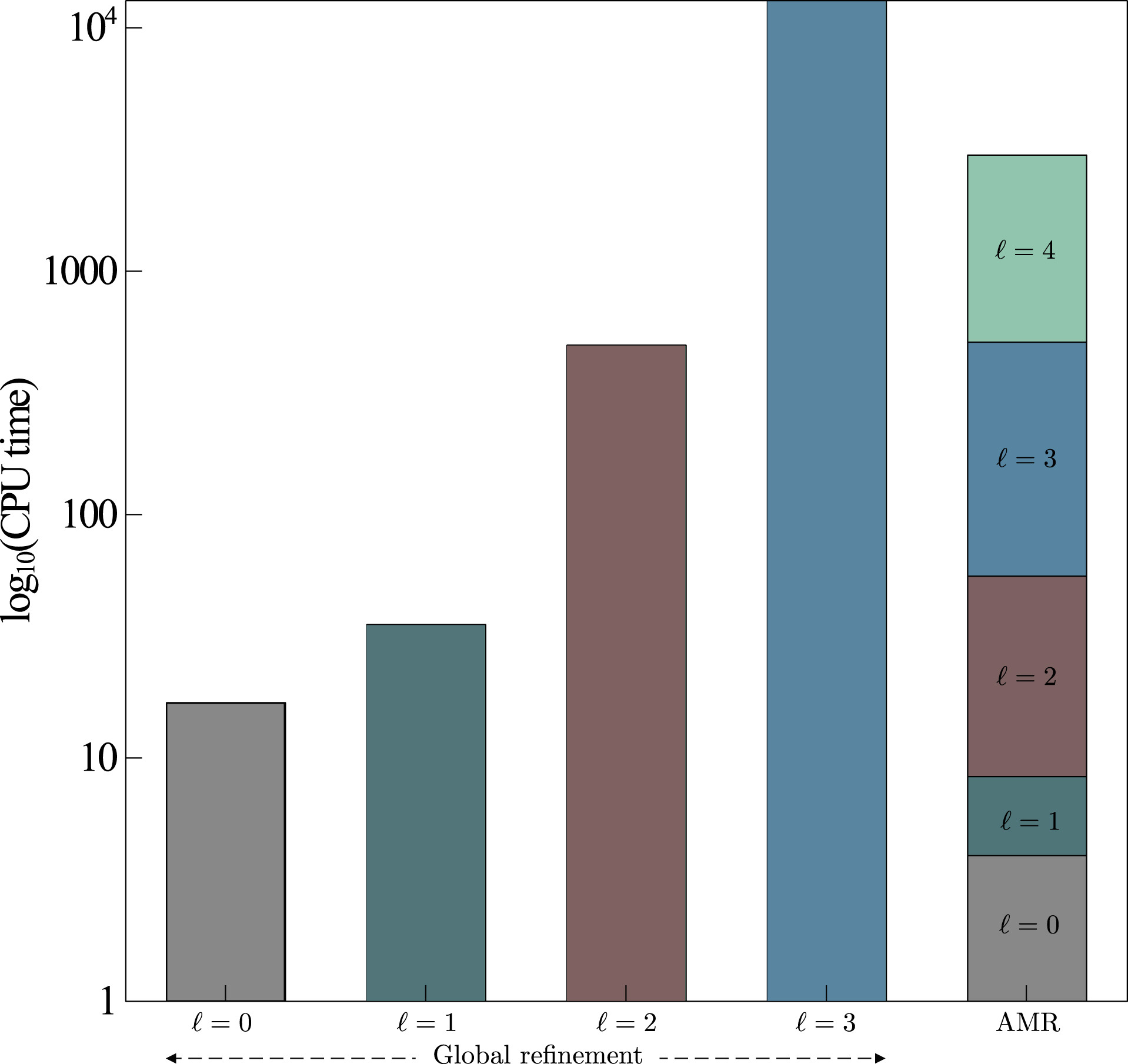
Reduction in CPU time compared to global refinement
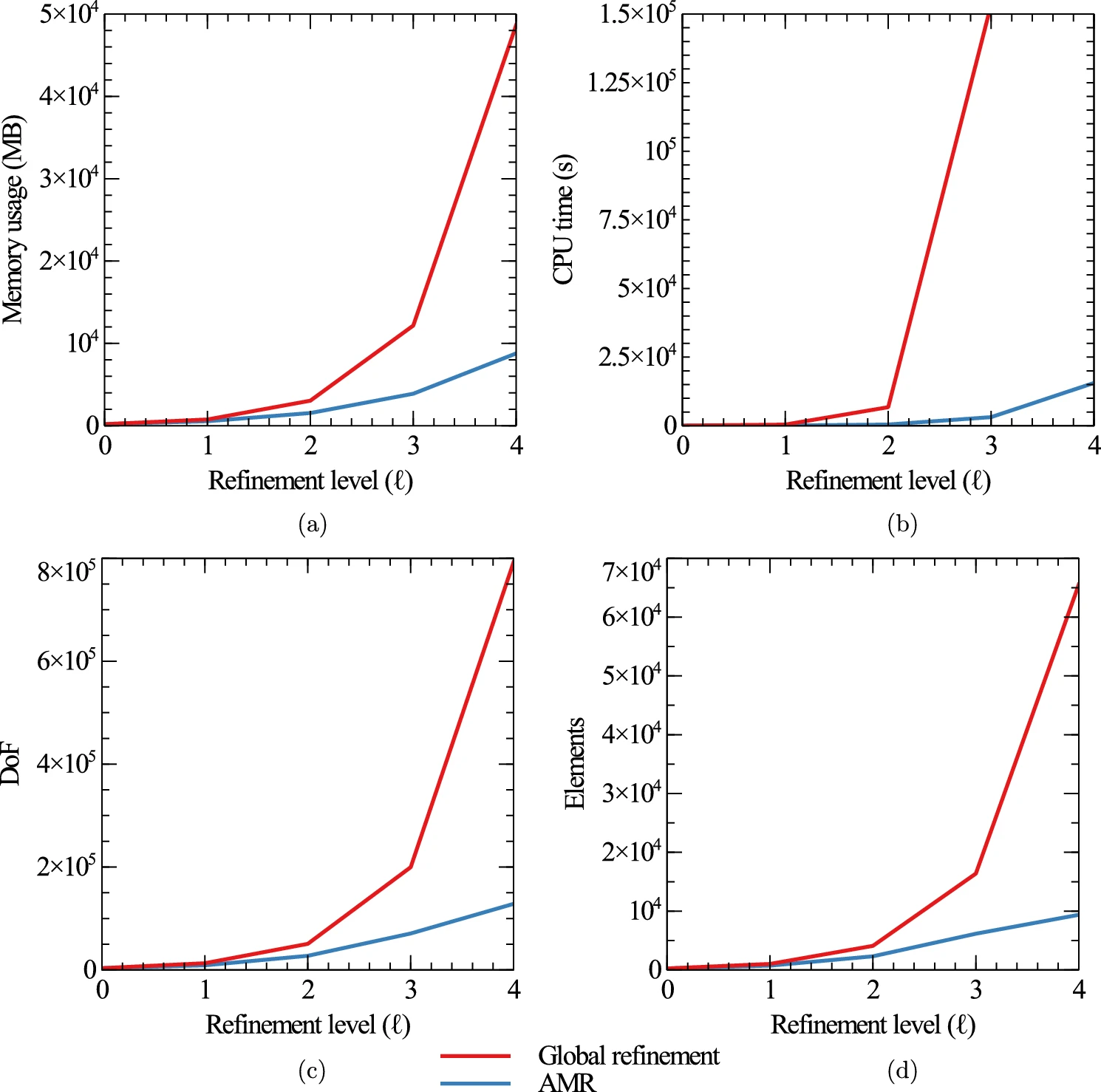
Reduction in all computational parameters in comparison to global refinement
Key Contributions
- Adaptive refinement strategies tailored for optimization problems
- Coupling of AMR with sensitivity analysis
- Reduced computational effort without compromising design quality