Auxetic Topology Optimization using IGA
(ongoing project)
1. The Material Hierarchy
In traditional engineering, we often work with what nature provides. However, the modern frontier lies in “architected” materials where the physical properties are a result of geometry rather than just chemical composition.
Natural vs. Architected Materials
- Natural Materials: Most materials (rubber, steel, bone) have a positive Poisson’s ratio (v > 0). When you stretch them, they become thinner in the cross-section.
- Architected Materials (Metamaterials): These are man-made solids where the macroscopic properties are derived from a specifically designed microstructure or “unit cell.”
What are Auxetic Materials?
Auxetic materials are a fascinating class of metamaterials with a Negative Poisson’s Ratio (NPR). Unlike conventional materials, when you pull an auxetic material, it expands laterally (becomes thicker).
2. Microstructure and Benefits
The “magic” of an auxetic material happens at the microscopic level. By repeating a specific geometric pattern—the unit cell—we can dictate how the entire structure reacts to stress.
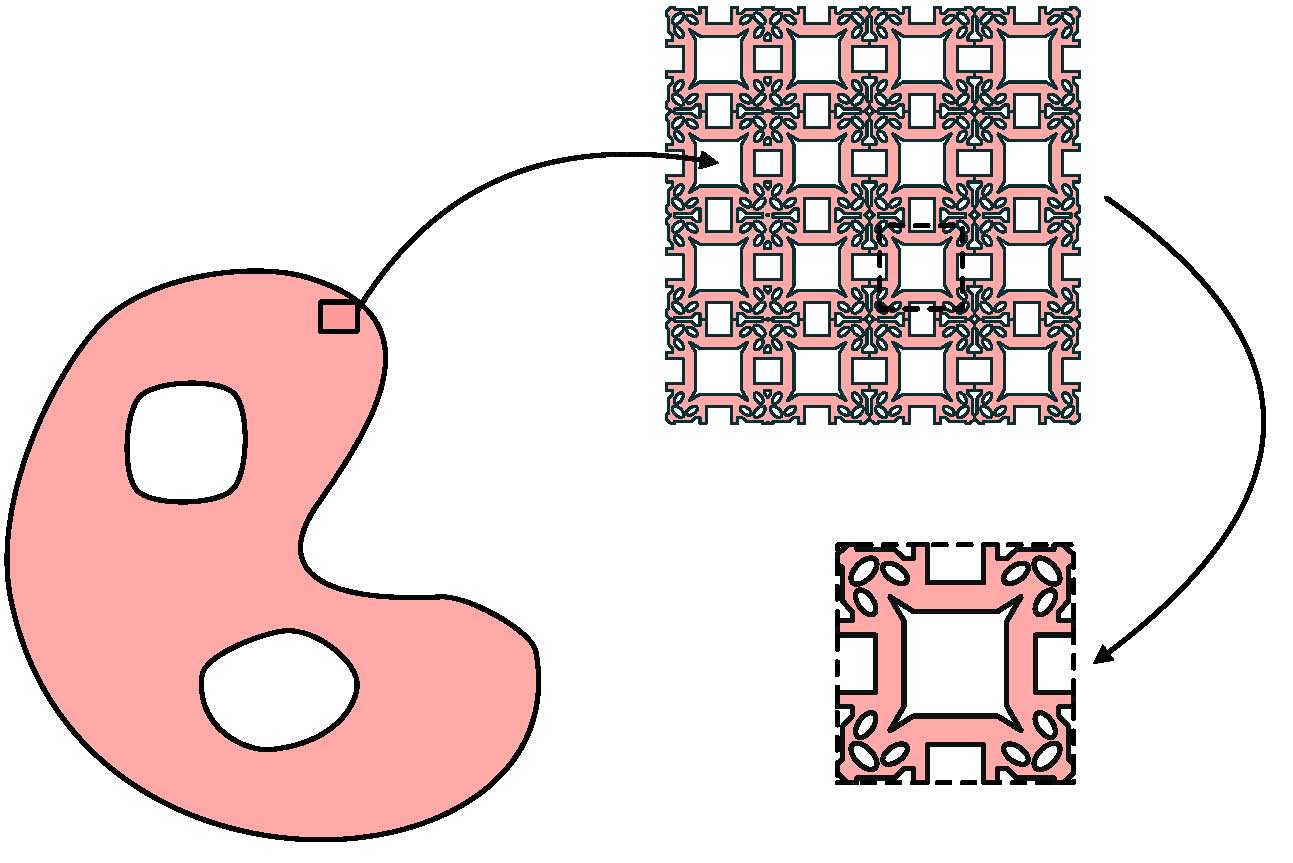
Common Microstructures
- Re-entrant Honeycombs: Hexagons with inward-pointing ribs.
- Rotating Polygons: Squares or triangles connected at vertices that rotate when pulled.
- Chiral Structures: Circular nodes connected by ligaments that “wrap” or “unwrap.”
Key Benefits & Applications
| Benefit | Explanation | Use Case |
|---|---|---|
| High Energy Absorption | They densify under impact rather than spreading out. | Body armor, vehicle bumpers. |
| Fracture Toughness | The material “crowds” around a crack tip, preventing it from spreading. | Aerospace components. |
| Synclastic Curvature | They naturally form dome shapes when bent (unlike the “saddle” shape of foam). | Medical stents, wearable tech. |
| Variable Permeability | Stretching the material opens up pores. | Smart filters, drug delivery. |
3. Generating Auxetics: Topology Optimization
Creating these materials manually is difficult. Instead, we use Topology Optimization (TO)—a mathematical approach that optimizes material layout within a given design space to meet specific performance targets.
To generate an auxetic, the optimization goal (objective function) is usually to minimize the Poisson’s ratio (v) until it becomes negative, subject to constraints like volume fraction (how much material we can use).
Traditional Topology Optimization uses Finite Element Analysis (FEA), which often results in “jagged” or “pixelated” edges (checkerboard patterns) that are hard to manufacture. This is where Isogeometric Analysis (IGA) changes the game. IGA uses the same mathematical basis functions—typically NURBS (Non-Uniform Rational B-Splines)—for both the design of the geometry and the analysis of its stress/strain.
Advantages of IGA in Auxetic Design:
- Smooth Boundaries: IGA naturally produces smooth, continuous curves. This is critical for auxetics, as sharp corners in microstructures act as “stress concentrators” that lead to failure.
- Higher Accuracy: It provides more precise results for the same computational cost compared to traditional mesh-based FEA.
- Seamless CAD Integration: Since the results are already in NURBS format, the optimized auxetic unit cell can be sent directly to 3D printers or CAD software without “re-drawing” the mesh.
4. Methodology
The goal is to minimize the function $f(\theta)$, which is designed to favor auxetic behavior by manipulating the effective elasticity properties:
\[\min_{\theta} f(\theta) = U_{1122}(\theta) - \beta^{l} \left( U_{1111}(\theta) + U_{2222}(\theta) \right)\]where
- $\theta$: The design variable representing the material density at a specific point or element.
- $U_{1122}, U_{1111}, U_{2222}$: Components related to the homogenized elasticity tensor (representing lateral and longitudinal stiffness).
- $\beta^l$: A weighting factor that controls the trade-off between different stiffness components.
- $k$: The target volume fraction (e.g., 0.3 for 30% material usage).
- $V_0$: The total volume of the design domain \Omega.
- $p$: The penalization power (typically p=3) used to drive the design toward “black and white” (solid or void) solutions.
The properties are calculated using a penalized density approach (similar to the Solid Isotropic Material with Penalization or SIMP method). The elemental and global strain energy components are defined as follows:
5. Representative results

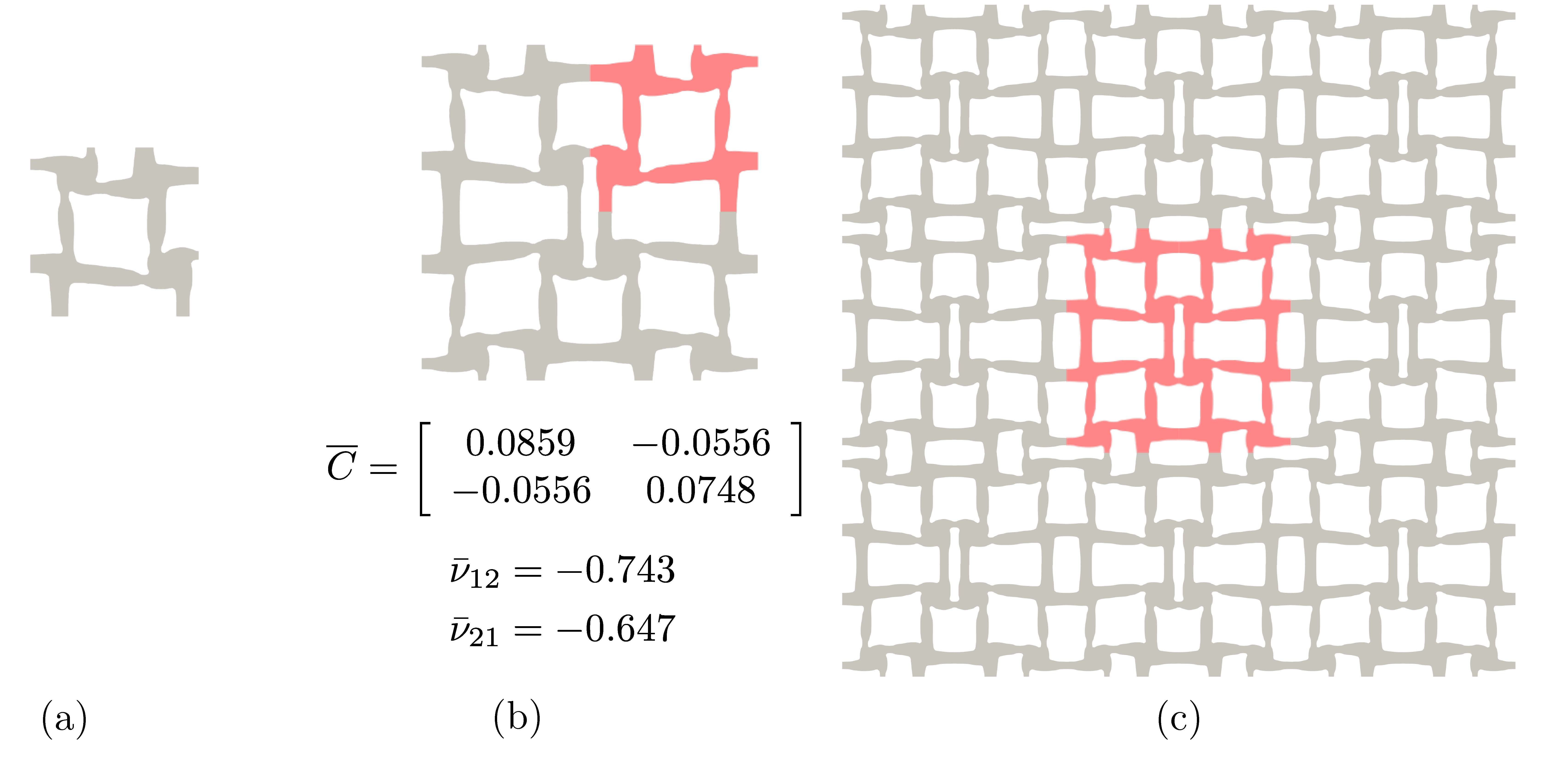
Key Contributions
- IGA-based framework for auxetic topology optimization
- Energy based homogenization methods